Gaussian processes

Gaussian processes GPs are a convenient way of defining priors over unknown functions: in an inference problem, they allow you to state that a function is smooth, without assuming a specific form (in other words, they allow non-parametric inference in a Bayesian setting).

The figure below shows samples from a GP, interpreted as a prior distribution: we have a an unknown function \(f(x)\) and all we wish to state is that \(f\) is smooth. The next panel shows a posterior distribution: we have a few noisy measurements of \(f\) (\(y_1 \ldots y_n\), and the black lines are samples from the posterior distribution, \(p(f|y_1 \ldots y_n)\). The beauty of GPs is that the posterior distribution is again a GP, but one constrained to lie close to the measured values.

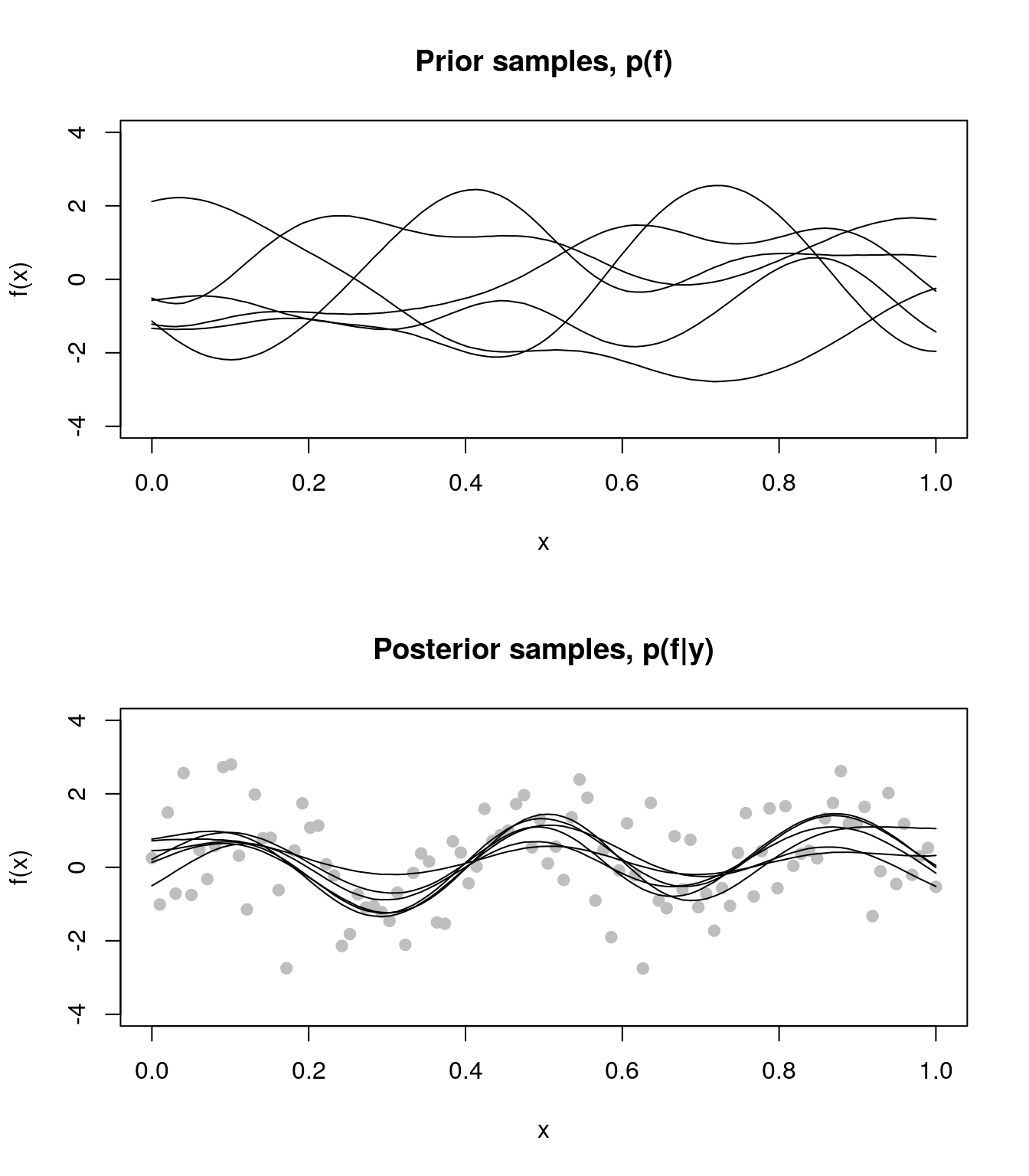
For more on GPs see the wonderful book by Rasmussen & Williams, Gaussian Processes for Machine Learning.

Challenges

GPs are notorious for scaling badly when the number of observations increases, with a cost in \(\mathcal{O}(n^{3})\). There are dozens of approximations attempting to reduce cost, and one of the most successful is based on a sparse approximation of the inverse covariance matrix (that’s the method implemented in INLA, and described in Lindgren et al. 2011). The theoretical underpinnings are somewhat complicated and rely crucially on seeing the GP as the solution of a stochastic Partial Differential Equations.

Unfortunately, this limits the applicability of the method to low-dimensional manifolds, but GPs are much more generic: as soon as you can define a covariance function over a space, you can define a GP over a space. Thus, one can have GPs over spaces of graphs, of strings, etc.

The goal of the GenGP project is to generalise the sparse-inverse approach to GPs.

Applications

So far we have worked a lot on Determinantal Point Processes, which are very tightly connected to GPs.

People

Ronald Phlypo Konstantin Usevich

On DPPs I work closely with Nicolas Tremblay and Pierre-Olivier Amblard.